Need help on force analysis on FBD
Moderators: justTripn, Elessar, dark_rain
Need help on force analysis on FBD
Ok, I'm embarressed to be asking this here, but if anyone can remember how to do this I'd definately appreciate the help. I'm doing an analysis of the forces being exerted on a slide by a kid who weighs 100 pounds = 45.359 kg, who's situated mid-way between the upper and lower supports. With a safety factor of 2, I've determined a total force of 889.94 N. The slide is at an angle of theta and of length L, both of which are undetermined variables for the time being. The coordinate system is set up so that the x-axis is parallel to the slide surface. Right, so I have no freakin' clue how to determine the reaction forces at the supports at either end. If it was a flat beam, it'd be pretty easy, but I can't remember any of the equations for doing it when the forces are at an angle to the coordinate system. Can anyone help me out?
Re: Need help on force analysis on FBD
You have to express the reaction forces at the two points as vector components, ya know w/ sin0 and cos0 (where 0 is theta). One sec while I draw somethin up.
Wait, did you want your reaction force components in the up and down direction or parallel to the axis? It changed how I do the arithmetic but not the basic problem.
I'm gonna have to pause until you get back to me, but maybe this advice will help:
Once you decide if your reaction forces are parallel to the axis or not, do a sum of forces in the x and y direction (and I'm assuming this is a static system, which means acceleration is zero, so forces sum in each direction to 0).
Now, once you do that you'll have two equations and 4 unknowns - 4 because A and B being the supports, each has a component in the x and y direction. I forgot for a second how you get the other 2 equations necessary, but I believe it's by summing moments to zero.
Sum the moment of rotation about teach point to be zero (because you want zero rotation in a static system... don't want this sliderotating over and crushing the kid, lol). I forget what the moment equation is but it's like force times moment arm length I THINK. M = Fd? Sounds right.
So you got 4 equations, 4 unknowns (you're gonna need to know theta, L, and the kid's mass).
And you're gonna have to define the length of the slide as x = L/cos(0) or the length up the slide that the kid is sitting as x = L/2cos(0) -- you're gonna need that number when computing the moment generated by the kid's weight.
Sorry I'm not gonna do a picture, I gotta go eat... but I hope that helps.
Have you had linear algebra or learned how to solve simultaneous sets of equations with a matrix? If you haven't, and you're in a Statics class, ask your professor - for one thing, it's a very elegant way to solve simultaneous sets of eqns even if you do the matrix method by hand, and for another thing, every single TI series calculator can solve an n x n matrix for you, aka, it'll take 10 seconds on teh calculator instead of 15 minutes by hand.
Wait, did you want your reaction force components in the up and down direction or parallel to the axis? It changed how I do the arithmetic but not the basic problem.
I'm gonna have to pause until you get back to me, but maybe this advice will help:
Once you decide if your reaction forces are parallel to the axis or not, do a sum of forces in the x and y direction (and I'm assuming this is a static system, which means acceleration is zero, so forces sum in each direction to 0).
Now, once you do that you'll have two equations and 4 unknowns - 4 because A and B being the supports, each has a component in the x and y direction. I forgot for a second how you get the other 2 equations necessary, but I believe it's by summing moments to zero.
Sum the moment of rotation about teach point to be zero (because you want zero rotation in a static system... don't want this sliderotating over and crushing the kid, lol). I forget what the moment equation is but it's like force times moment arm length I THINK. M = Fd? Sounds right.
So you got 4 equations, 4 unknowns (you're gonna need to know theta, L, and the kid's mass).
And you're gonna have to define the length of the slide as x = L/cos(0) or the length up the slide that the kid is sitting as x = L/2cos(0) -- you're gonna need that number when computing the moment generated by the kid's weight.
Sorry I'm not gonna do a picture, I gotta go eat... but I hope that helps.
Have you had linear algebra or learned how to solve simultaneous sets of equations with a matrix? If you haven't, and you're in a Statics class, ask your professor - for one thing, it's a very elegant way to solve simultaneous sets of eqns even if you do the matrix method by hand, and for another thing, every single TI series calculator can solve an n x n matrix for you, aka, it'll take 10 seconds on teh calculator instead of 15 minutes by hand.
"I call shotgun!"
"I call nine millimeter." - John and Cameron
Favorites:
Vulcan For...
Your Mom n' Me
"I call nine millimeter." - John and Cameron
Favorites:
Vulcan For...
Your Mom n' Me
Re: Need help on force analysis on FBD
Here's the free body diagram:


Re: Need help on force analysis on FBD
yep, looks good. Just sum forces and moments. Just rember that R1 and R2 have two vector components. If your question is how you get those vector components, it's hard to explain in words but, you can make a similar triangle out of the R1 and R2 such that there's a theta (the same theta as in the big triangle) in there and you can make a trig relation work. Like R1x = R1cos(theta) or something. I'm not sure if that's right, I'd have to draw it out to be sure, but that's teh general idea.
EDIT: Ok nevermind i'll just tell ya: It looks like R1 is R1y = R1 cos(0) and R1x = R1 sin(0)
See how I got that? Draw an arrow meeting at the point R1 that is pointing parallel to the Y axis and draw your triangle such that R1 itself, the magnitude, makes the hypotenuse of that triangle. The angle between the line parallel with Y and the R1 hypotenuse then will be theta, and your R1y component is R1 cos(theta). Same process for R2.
Looks like you already know how to do that similar triangle business because you made one with the kid's weight.
Oh and I'm not sure but should your moment rotations be defined in the same direction? Idk if it matters. It would just be convention.
Make sense?
EDIT: Ok nevermind i'll just tell ya: It looks like R1 is R1y = R1 cos(0) and R1x = R1 sin(0)
See how I got that? Draw an arrow meeting at the point R1 that is pointing parallel to the Y axis and draw your triangle such that R1 itself, the magnitude, makes the hypotenuse of that triangle. The angle between the line parallel with Y and the R1 hypotenuse then will be theta, and your R1y component is R1 cos(theta). Same process for R2.
Looks like you already know how to do that similar triangle business because you made one with the kid's weight.
Oh and I'm not sure but should your moment rotations be defined in the same direction? Idk if it matters. It would just be convention.
Make sense?
"I call shotgun!"
"I call nine millimeter." - John and Cameron
Favorites:
Vulcan For...
Your Mom n' Me
"I call nine millimeter." - John and Cameron
Favorites:
Vulcan For...
Your Mom n' Me
Re: Need help on force analysis on FBD
How do I separate the main force between R1 and R2 though? R1 is going to be the larger of the two because that's where most of the kid's weight is going, but R2 is also going to be supporting some of it.
Re: Need help on force analysis on FBD
Well the kid's weight causes forces at both reaction points. The way I learned how to do these problems, you sum all forces in the x direction and then all in the y direction an set it equal to zero. Like this:
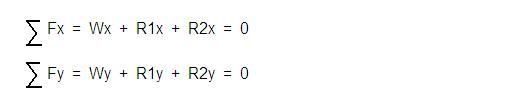
That's not including the moment sums, but that's because I remembered something else, any time you sum moments, you are summing them about a certain point, now naturally, you're gonna sum about the points where R1 and R2 are reaction forces for (call em A and B), but I just didn't write it out b/c I didn't feel like computing the moment arms.
Now, the kid's weight is going to be mg cos0 or mg sin0 depending on the geometry. And it'll prrrrrrrobably be negative, because the kid's weight force is pointing in the negative y and negative x direction.
To answer your question... the kid's weight causes reaction forces on both points. You don't really approach the problem by asking 'how do you divide it between them' but rather, how does his force effect the whole system. Using those sums of forces, and two more eqns for moments, you can solve for R1x and R1y (and then get R1 = sqrt( R1y^2 + R1x^2) ) and then solve for R2x and R2y, and get the magnitude of R2 the same way, sqrt of the sum of the squares.
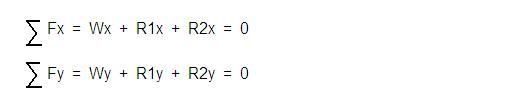
That's not including the moment sums, but that's because I remembered something else, any time you sum moments, you are summing them about a certain point, now naturally, you're gonna sum about the points where R1 and R2 are reaction forces for (call em A and B), but I just didn't write it out b/c I didn't feel like computing the moment arms.
Now, the kid's weight is going to be mg cos0 or mg sin0 depending on the geometry. And it'll prrrrrrrobably be negative, because the kid's weight force is pointing in the negative y and negative x direction.
To answer your question... the kid's weight causes reaction forces on both points. You don't really approach the problem by asking 'how do you divide it between them' but rather, how does his force effect the whole system. Using those sums of forces, and two more eqns for moments, you can solve for R1x and R1y (and then get R1 = sqrt( R1y^2 + R1x^2) ) and then solve for R2x and R2y, and get the magnitude of R2 the same way, sqrt of the sum of the squares.
"I call shotgun!"
"I call nine millimeter." - John and Cameron
Favorites:
Vulcan For...
Your Mom n' Me
"I call nine millimeter." - John and Cameron
Favorites:
Vulcan For...
Your Mom n' Me
Who is online
Users browsing this forum: No registered users and 6 guests


